Beware the GDP
We have to stop thinking that crude estimates of a platonic concept we call GDP are factual information
If you log on to the “Economic Growth” page of “Our World in Data” it is easy to access estimates of GDP for over a hundred countries for the last two thousand years. These estimates are presented as fact. For example, right at the beginning of the first section titled “The history of economic growth” it says in the third paragraph:
Average incomes (as measured by GDP per capita) in England between the year 1270 and 1650 were £1,051 when measured in today’s prices.
That is, we talk about these estimates as if we had a time machine, traveled to England every year from 1270 to 1650, and “measured” their GDP using the exact same methods we use today.
In fact, asserting that “average incomes are (some small number) hundreds of years ago measured in today’s prices” is absurd on several levels:
Even today our official GDP figures are quite crude estimates produced by government agencies, despite massive resources involved in their estimation these figures are not something close to a “true” measure of economic output, and therefore they can vary substantially if you extract official figures from the same government agency at different times.
The reason why GDP figures are always varying is due to the fact that GDP is a concept based on abstract theoretical concepts that do not really exist in reality. In other words, GDP is not really a thing.
Historical GDP estimates are based on the projection of present estimates on very long time series that suffer from the inexistence of much of the required data, lots of noise, and mathematically unsolvable index-number issues.
Due to these issues, which are very serious issues, GDP is not a tool that should be used without extreme care. It is useful but it also can lead to very misleading conclusions.
The history of GDP
GDP is the main entry in an internationally standardized accounting system for national aggregates called the System of National Accounts (SNA).
This SNA came into being in the 1920s and 1930s, a time when thinking about economics in terms of national aggregates became popular thanks in no small part to the influence of the theories of John M. Keynes. Economists began to focus their attention on how to measure these aggregates, and these efforts culminated in our modern SNA in the United States during the Great Depression.
During the Depression, many industries in the United States were seeing their revenues and employment collapsing, so the US government assembled a team of experts to construct an index of national production to get an idea of “what the hell is going on” for the economy of the country as a whole. This index of national production is what we today call GDP or “Gross Domestic Product”, although the terms “GNP” or “gross national product” and “NI” or “national income” were often used in the past (these three concepts are very close in accounting terms as, typically, the variation across them consists only of a few percentage points).
The theory underlying GDP as a concept
The theoretical framework behind the concept of GDP is based on quite strong assumptions. They are the following:
There exists a well-defined set of “final goods” that constitute the whole set of goods any person would value.
The output of each of these final goods is transacted at market prices that are identical across the whole country and period of analysis (usually a year or a quarter).
Each of these market prices exactly matches their marginal costs of production (that is, markets operate in perfect competition).
The marginal costs of production are determined by production technology that satisfies the condition that we can increase and decrease the output in proportion to the variation of the quantities of workers and capital goods involved in their production (that is, satisfies constant returns to scale and convexity).
To get an understanding of what Assumption (4) means, it says that if you produce cars with workers and generic “machines”, then if you vary the number of workers and these “machines” by 10% then the output will also change by 10% and this should also true for variations of 2-3-5-15-20-30%, etc.
Given these assumptions, we can multiply the quantities of each of the final goods (which exist and are well defined by assumption 1) produced inside the country during the period of analysis by their prices (by assumption 2, market prices are the same across time and space) and we get the value of gross output for the country as a whole for that period. As these prices match the marginal costs of production it means that GDP is a measure of the economy's productive capacity: if you decrease the output of one good and allocate the factors of production to produce another good, assumptions (3) and (4) guarantee that the value of GDP stays the same. That is, GDP is then an accurate measure of the size of “the economy” and not just a number made up of quantities of an arbitrary set of goods multiplied by prices.
To measure the change or “economic growth” of GDP from, let us say, period 1 to period 2, we take the GDP figures of period 1 and period 2 and normalize the value in constant currency units, that is, we either use prices of period 1 to measure GDP in period 2 or use prices in period 2 to measure GDP in period 1. If the prices of the goods in these two periods are not perfectly proportional then GDP measured according to period 1 or period 2 prices will be different.
This discussion implies that even if assumptions (1), (2), (3), and (4) hold, it is not true that the “GDP growth rate” is actually a well-defined thing as it can vary depending on the method you use to compute it. Some people think that the geometric average of these two estimates (that is, the GDP measured on prices of periods 1 or 2), called the Fisher ideal index, is the best way to measure GDP growth rates. Therefore, if we have GDP figures for periods 1 to N, there are three different methods of computing the change in GDP between any pair of periods and there is no restriction on which periods you can use to measure the growth from period 1 to N: you can measure the growth from period 1 to period 3 using prices from period 2, then you can use the geometric average of prices from periods 3 and 7 to measure growth rate up to period 7, then you can use prices from period 7 to measure growth up to period 10, etc. As the number of periods increases, the number of different GDP growth rates that can be measured quickly increases to infinity.
Implementation of the theory in official GDP estimates
As we have seen, even in a world that perfectly fits the assumptions required of the concept of GDP, there is no such thing as the “correct” GDP growth rate. In addition, we can find many problems with confronting reality to the assumptions (1),(2),(3), and (4) when we confront then with reality.
Assumption (1). In reality, it is not true that there exists a universally agreed set of goods that we all regard as final goods. For example, one person might be indifferent between two apartments in the same city while another person might not. These two apartments are two units of one good for someone and two goods for someone else. This means for example, that when we compute the change in GDP from period 1 to period 2, we are assuming that everybody agrees that one apple in period 1 is the same good as one apple in period 2.
In addition, a person’s preferences change over time which means that maybe the same person might perceive that these two apartments were in fact different goods. Therefore, there are as many goods as one person can perceive times the number of times the perceptions of that person change, times the number of people in the world. This essentially implies that the set of final goods is not well defined in practice, and the subjective opinion of the people running statistical offices determines what this set is supposed to be when they calculate GDP.
There is also the fact that classifying a good to be either a final good or an intermediate good is ultimately subjective. For example, formal clothing such as a suit and a tie can be regarded as an intermediate good as many people wear these clothes for their professions, not because they like wearing them. Thus, sales of formal clothing could be regarded as an intermediate input for the legal industry for example. Classification often depends on whether a good is considered durable or non-durable, which is also subjective.
In addition, technological change means that many goods we consume today did not exist even a couple of decades ago. How do we account for these goods? The construction of GDP according to theory assigns for these goods the output of zero for all the periods before they were invented, but their market prices must have somehow existed for these periods to be able to measure the economic output relative to periods in which output included these goods.
In practice, national offices just ignored the change in the set of goods to measure GDP: they used only the prices of the goods that existed across time.
In recent years, as economists complained about this, statistical offices construct these hypothetical prices using what people call “hedonic methods”, which just basically means for example they compare the prices of an old TV that stopped being manufactured in 2010 with a new model that entered the market in 2010 and this price ratio determines the estimated price for this hypothetical good in earlier periods until the old TV stopped being manufactured as well, in suppose 1997, but this old TV had a price in the time it started being manufactured which we use to compare with an even older model which was manufactured up to 1989, then we carry over that price. We end up with a modern LED TV being “measured” in the US GDP as being equal to 100 black and white TVs from the 1960s. This procedure now applies to most goods: a car sold today is measured as equal to several cars sold a few decades ago in terms of GDP.
Thanks to hedonic methods being adopted by the US’s statistical office that “measures” the GDP, the official growth rates of the US’s economy increased a lot. In developing countries, like Brazil and Mexico, their official GDP growth rates do not include any such adjustment for technological change, and for these two countries as well as many other Latin American countries, their growth rates are similar to the US’s in recent decades. This similarity in growth rates prompted economists to declare the existence of a “middle-income trap” that has afflicted Latin America, as economic theory predicts that the GDP of countries like Brazil and Mexico should grow faster than in the US.
Assumption (2). It is not true that all of GDP is sold at market prices. A large fraction of GDP that is estimated by statistical offices consists of some degree of self-sufficient production that is included (imputed house rent and agricultural output consumed by households in developing countries), and imputed values of government services. These imputations are either estimated—the value of imputed house rent is based on how much it would perhaps be worth in the rental market—or costs are assumed to equal value: for example, US military expenditures of around 750 billion dollars count in GDP as services with a market value assumed to be 750 billion. Roughly around 70-75% of the GDP of most countries consists of estimates of actual market transactions. In the past, this proportion was far smaller—in 13th century England about 95% of the population lived in the countryside and most food people ate was the food they grew.
In reality, prices vary a lot across a given time period (let us say, a quarter or even a month) in a given location (a city):
Considering GDP involves the assumption of uniform prices across a whole country, assumption (2) fails spectacularly. Assumptions (1) and (2) interact here: there is a lot of price dispersion in reality partly because people do not think a bottle of ketchup sold two blocks down the street is exactly the same good as a bottle of ketchup sold next door.
Multiplying estimated quantities of a poorly defined set of “final goods” with average prices measured by statistical agencies does not yield precise figures either. The official GDP of the UK in 1990 in millions of pounds from that same year varied by over 20% depending on the date on which you download the data from their website:
662,850 (reported by the Bank of England 2017)
615,673 (reported by the World Bank 2018)
570,283 (reported by Piketty & Zucman 2014)
554,486 (reported by Maddison 2003)
In developing countries, the size of the official GDP can change by much as 60% (Ghana) or 94% (Nigeria) after an update (see Coyle 2020). Updates of national accounts tend nearly always to increase the official size of GDP, rarely decrease it, which suggests that official GDP is not a non-biased estimate of the “true GDP”, in fact such “true GDP” does not exist at all.
Assumption (3). The assumption of perfect competition is quite strong as it requires that competition across firms be so strict that any firm that raises prices a little bit above their cost (“cost” here includes operating costs and the expected return on the firm’s capital) will turn away all their consumers and go bankrupt. Still, it actually has stronger theoretical foundations than Assumptions (1) and (2) as there are indeed many firms competing in most industries, so rational consumers would not purchase from one firm if their price would be substantially increased.
Empirically, however, it appears that industries have varying levels of competitiveness which means that the correlation of market prices with the costs of production is not perfect, as required for the concept of GDP to work.
Assumption (4). This is one of the most reasonable of all assumptions for large economies. The reason is that as the world economy is big, the size of demand for even the most sophisticated products allows output to vary without changing the production cost due to scale effects.
Let me give an example, in the motor vehicle industry, one of the most technically sophisticated industries that require big investments to reach the optimal scale of production, the optimal plant capacity is reached at around 100-200,000 motor vehicles per year, as global sales are around 100 million, therefore variations as small as 0.1% in output can occur without changing marginal costs in the long-run.
In small countries, this assumption does not hold. In a small country, a single plant often is the entire country’s industry for a certain good. In that case, any change in output means output deviates from the optimal scale of production for one plant that and will change production costs.
Historical GDP estimates: speculation treated as fact
The further back we go in time with real per capita GDP time series, the largest the incongruence of these “measured” GDP figures with direct empirical evidence and we do not need to go very back in time to get some grotesquely large discrepancies. In the Our World in Data webpage “Economic Growth,” their figure for Germany’s “measured” per capita income in 1937 amounts to 13.5% of America’s GDP per capita in 2018, a figure comparable to India’s GDP per capita for the same year which amounts to 12.3% of America’s. Is it plausible that the average Indian today has a standard of living that is the same as a typical German in the 1930s?
I choose 1937 because Broadberry and Burhop (2010) provide detailed statistics of prices and wages for Germany at that date. The average annual earnings of a worker were 1,850 marks, which includes the average earnings of agricultural workers which were estimated to be less than half of the urban workers. Urban workers typically earned about 2,100-2,200 marks per year. The problem is that the 1939 German census classified 58% of agricultural workers as “unpaid family helpers” thus these very low agricultural earnings are likely the consequence of dividing the aggregate agricultural wage bill across this population inflated by unpaid family helpers. Adjusting the national average upward by excluding these unpaid family helpers from the labor force yields an average income of ca. 2,000 marks, close to the average urban income. Rent was 7.24 marks per room per month, and a pound of potatoes, the biggest source of calories, was 0.03 marks, a pound of white bread was 0.14 marks, a pound of cheese was 0.42 marks, and a pound of beef was nearly 30 times as expensive as potatoes at 0.88 marks.
According to the BLS (Bureau of Labor Statistics), today American average earnings are 1,098.55 dollars per week, which is about 55,000 dollars per year. Potatoes are 0.82 dollars a pound, bread (white) is 1.61 dollars per pound, cheese is about 5.4 dollars a pound (natural, processed cheese is cheaper), and beef depending on the type is around 5 to 8 dollars per pound (take the average to be 6.5 dollars). Rent for a single-bedroom apartment in the city center is 1,669.47 dollars according to Numbeo (as BLS doesn’t have anything I could find to compare with a room) and 1,237.90 dollars outside of the city center, taking the mean of 1,450 and considering a single bedroom apartment can be taken to have 4 rooms means a monthly cost of a room at 360 dollars.
Thus, the 1937 German worker could rent 181% as many rooms as an American worker today, buy 99% as many potatoes, 42% as much bread, 47% as much “natural” cheese, and 26% as much beef. Compare these figures to the 13.5% per capita GDP “measured” in the Maddison dataset. Note also that the relative prices between rent and beef are different by a factor of eight. This is so thanks to technological change: US real estate became expensive over time as other goods became relatively cheaper, which means that estimated variation in GDP changes a lot depending on the method used to estimate it.
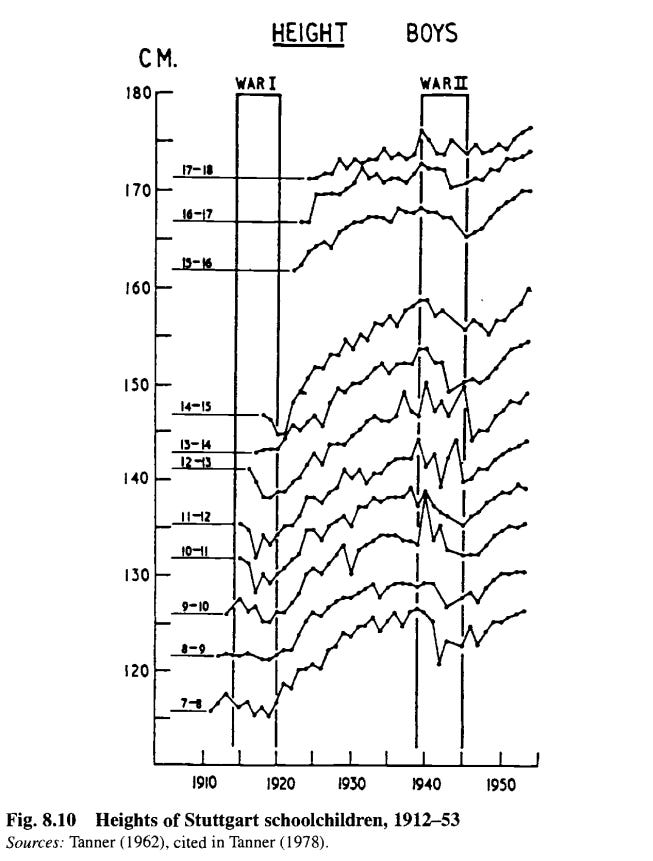
We measure nutritional standards using height data. In the US today, the average adult male height is 175.3 cm, in India average adult male heights are 10 cm shorter, at 165 cm. However, Indian men from the upper classes are 174.4 cm tall, and less than 1 cm shorter than Americans, which suggests the difference is not genetic but nutritional. For comparison, German 17-18 year old schoolkids were reaching 175 cm just before WW2:
One example of the issue we get from blindly trusting these GDP estimates is that some well-established statistical phenomenon that is observed with modern data disappears when we try to look at earlier periods. For example, Koyama and Rubin (2022) claim that there was no relationship 500 years ago between urbanization rates and income, based on this “data” from the Maddison Project.
Another common problem of projecting GDP for very long periods is that it yields relative income levels that are in direct contradiction with the evidence from that point in time. For example, Maddison (2010) estimated US GDP per capita to be only about half of the level of Britain in the early 19th century and only reached British levels around 1910. Then, Lindert & Williamson (2016) came up with estimates for the American colonial period that show American incomes were already much higher than British incomes by the late 18th century, diverging from the relative level of Maddison’s estimated incomes in the early 19th century by about 200%.
Conclusion
While it is obvious that we are far richer than we were in the past it is also rather obvious now that this improvement cannot be measured in a meaningful way using a single statistic. GDP can be useful as a tool to get an idea of the scale of economic fluctuations and can be useful to indicate if certain countries are developing at faster rates than others. It cannot be used to make claims such as “country X will converge to income of country Y in two decades if both grow at the current rate” or that “France in 1930 was poorer than Pakistan is today.”
References
Peter H. Lindert & Jeffrey G. Williamson, 2016. "American colonial incomes, 1650-1774," The Economic History Review, vol 69(1), pages 54-77.
Koyama, M. and Rubin, J. (2022), How the World Became Rich: The Historical Origins of Economic Growth. Polity; 1st edition.
Stephen Broadberry and Carsten Burhop 2010. Real Wages and Labor Productivity in Britain and Germany, 1871-1938: A Unified Approach to the International Comparison of Living Standards, The Journal of Economic History, Vol. 70, No. 2